Copyright © 2015-2016 Lester Hedges

About
A simple C++ library to implement the "virtual-move" Monte Carlo (VMMC) algorithm of Steve Whitelam and Phill Geissler, see:
- Avoiding unphysical kinetic traps in Monte Carlo simulations of strongly
attractive particles,
S. Whitelam and P.L. Geissler, Journal of Chemical Physics, 127, 154101 (2007)
We introduce a “virtual-move” Monte Carlo algorithm for systems of pairwise-interacting particles. This algorithm facilitates the simulation of particles possessing attractions of short range and arbitrary strength and geometry, an important realization being self-assembling particles endowed with strong, short-ranged, and angularly specific (“patchy”) attractions. Standard Monte Carlo techniques employ sequential updates of particles and can suffer from low acceptance rates when attractions are strong. In this event, collective motion can be strongly suppressed. Our algorithm avoids this problem by proposing simultaneous moves of collections (clusters) of particles according to gradients of interaction energies. One particle first executes a “virtual” trial move. We determine which of its neighbours move in a similar fashion by calculating individual bond energies before and after the proposed move. We iterate this procedure and update simultaneously the positions of all affected particles. Particles move according to an approximation of realistic dynamics without requiring the explicit computation of forces and without the step size restrictions required when integrating equations of motion. We employ a size- and shape-dependent damping of cluster movements, motivated by collective hydrodynamic effects neglected in simple implementations of Brownian dynamics.
- Approximating the dynamical evolution of systems of strongly interacting overdamped particles, S. Whitelam, Molecular Simulation, 37 (7) (2011). (Preprint version available here.)
Our primary goal is to make VMMC accessible to a wider audience, for whom the time required to code the algorithm poses a significant barrier to using the method. This allows the user to focus on model development.
The animation below shows a comparison of the dynamics generated by traditional single-particle Monte Carlo (SPMC) and the VMMC algorithm for a periodic two-dimensional square-well fluid. The model system consists of particles interacting via strong, short-ranged isotropic interactions. Due to the suppression of collective particle rearrangements, SPMC results in the slow Ostwald ripening of isolated clusters. In contrast, VMMC facilitates the diffusion and coalescence of particle clusters, resulting in a long-time dynamics that is dominated by the motion of a single large cluster. Both trajectories represent one billion trial moves of the respective algorithms, with the system initialised with a random, non-overlapping, particle configuration in each case.
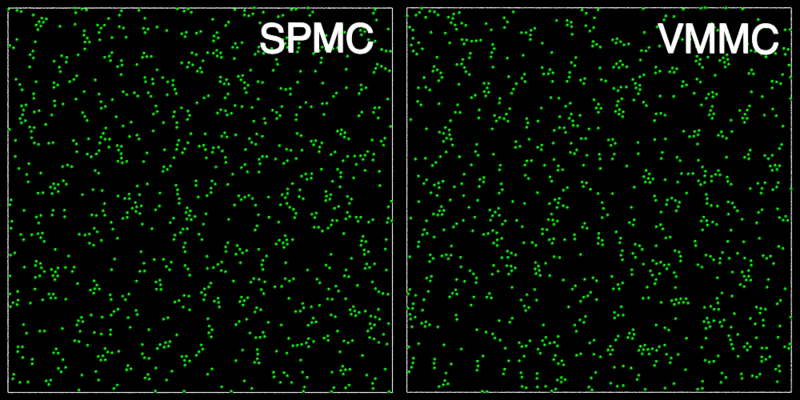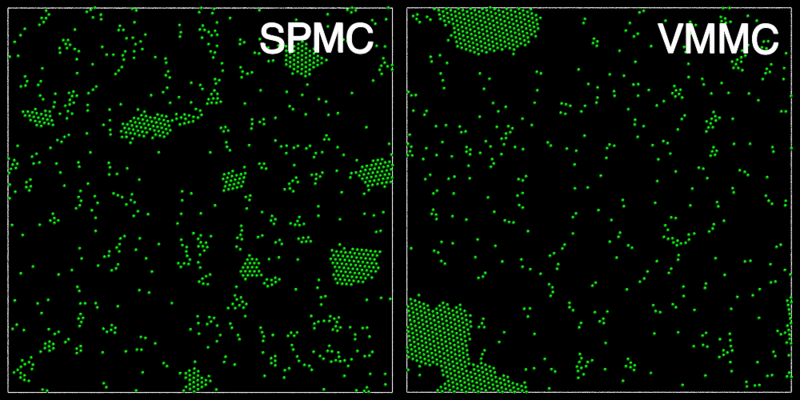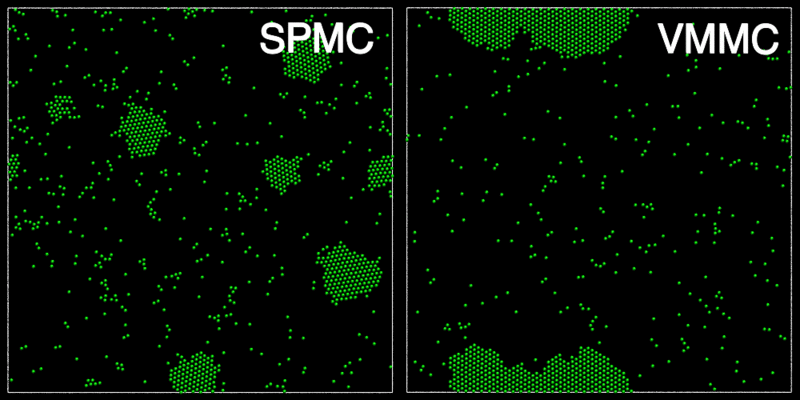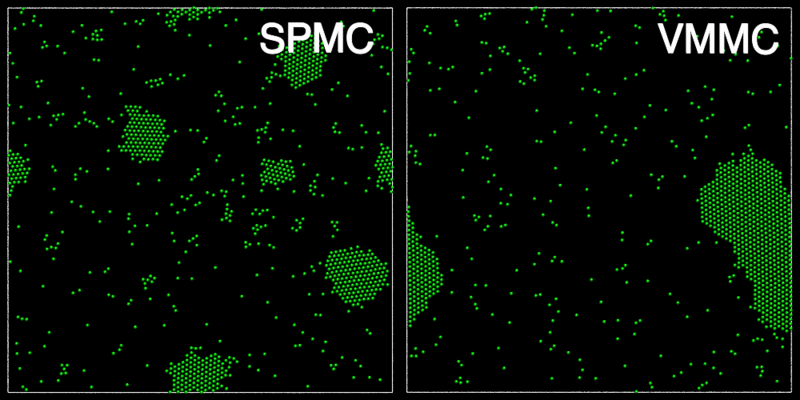
The VMMC algorithm works by proposing the move of a single, randomly chosen, "seed" particle. If, following the move, the change in the energy of interaction between the particle and its neighbours is unfavourable, then those neighbours are recruited and moved in concert. This process is iterated recursively for each new recruit until no further particles show a tendency to move.
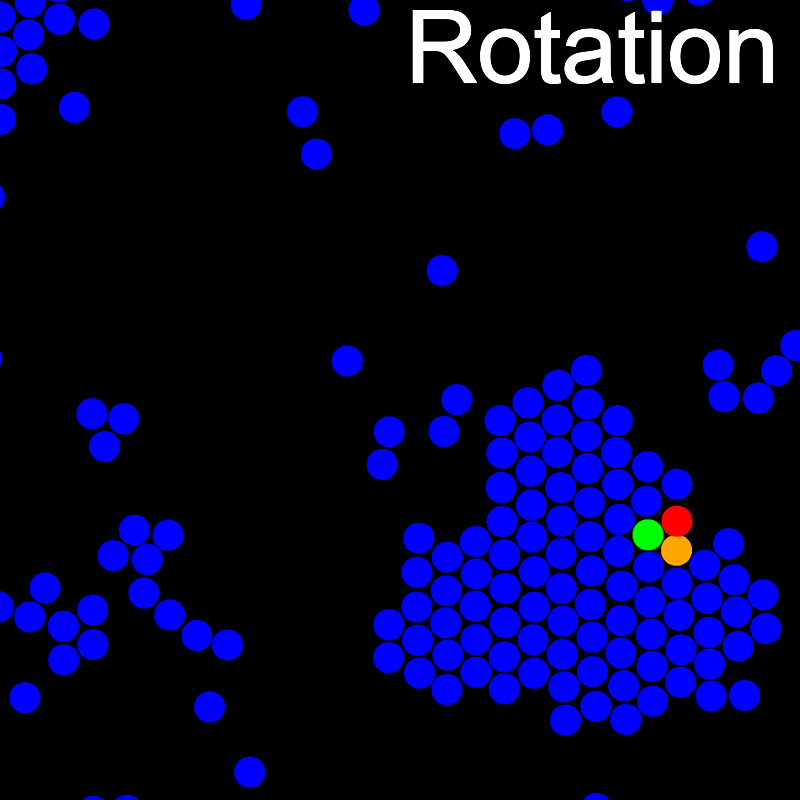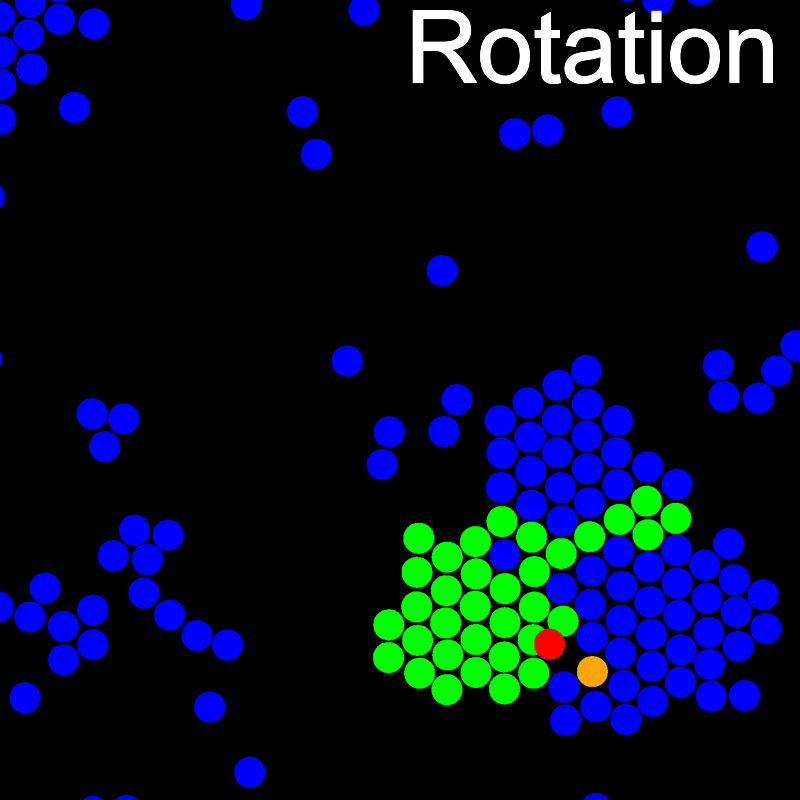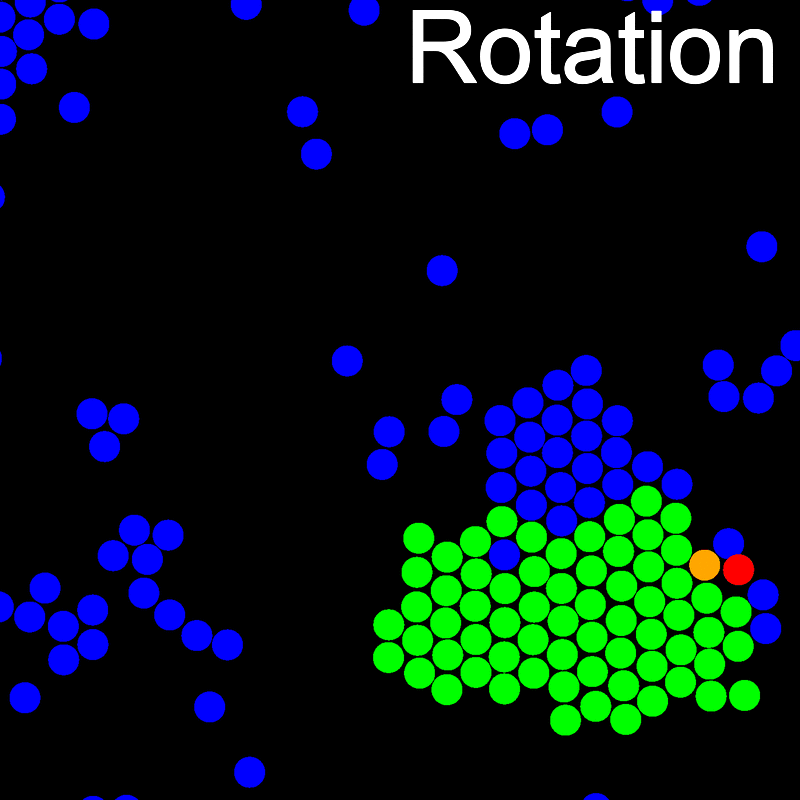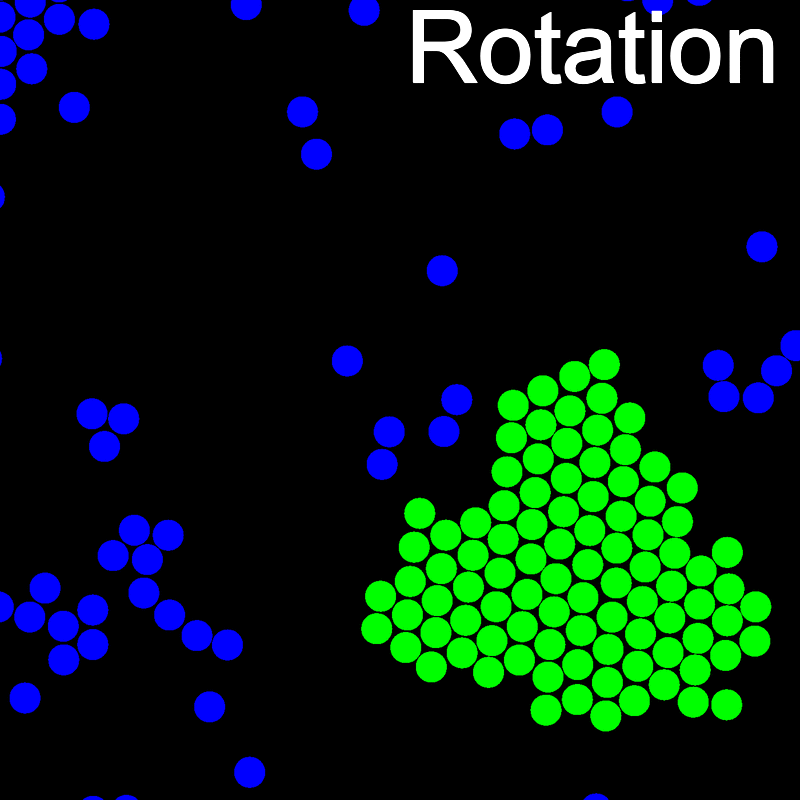
The animations below illustrate example VMMC translation and rotation moves taken from a real simulation. Red indicates the most recent recruit to the cluster, orange indicates the nearest neighbour to which link formation is currently being tested, and green indicates those particles that have been accepted as part of the cluster move. The animations show how a recursive depth-first search is used to iteratively link particles to the cluster. Particles are linked according to probabilities based on the pair interaction energy differences following the forward and reverse virtual move of each recruit. Computation of the reverse move is required to enforce superdetailed balance, thus ensuring that the probability of a given particle pushing or pulling on the cluster is the same.
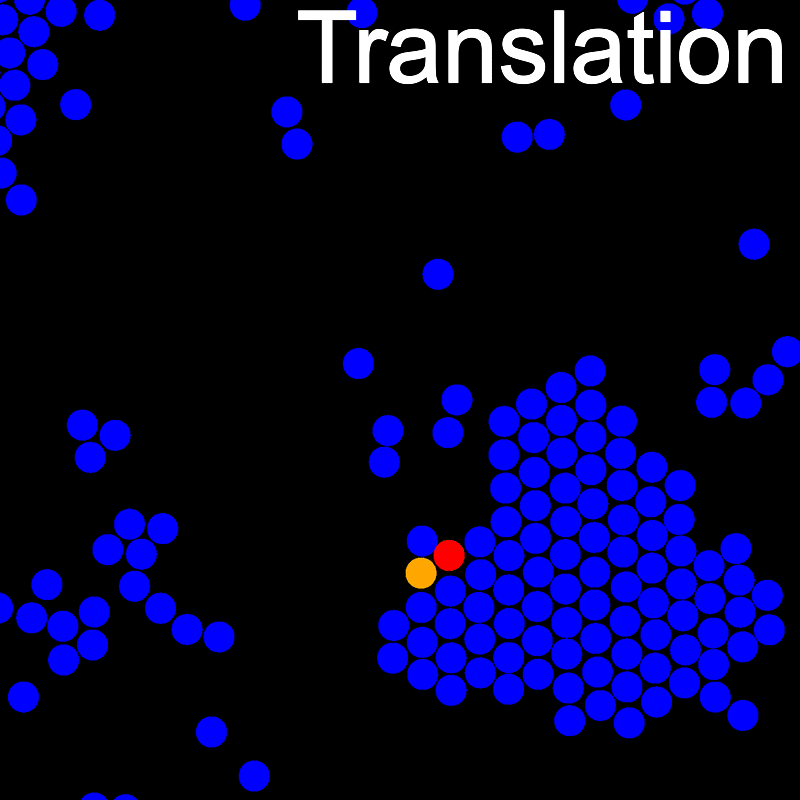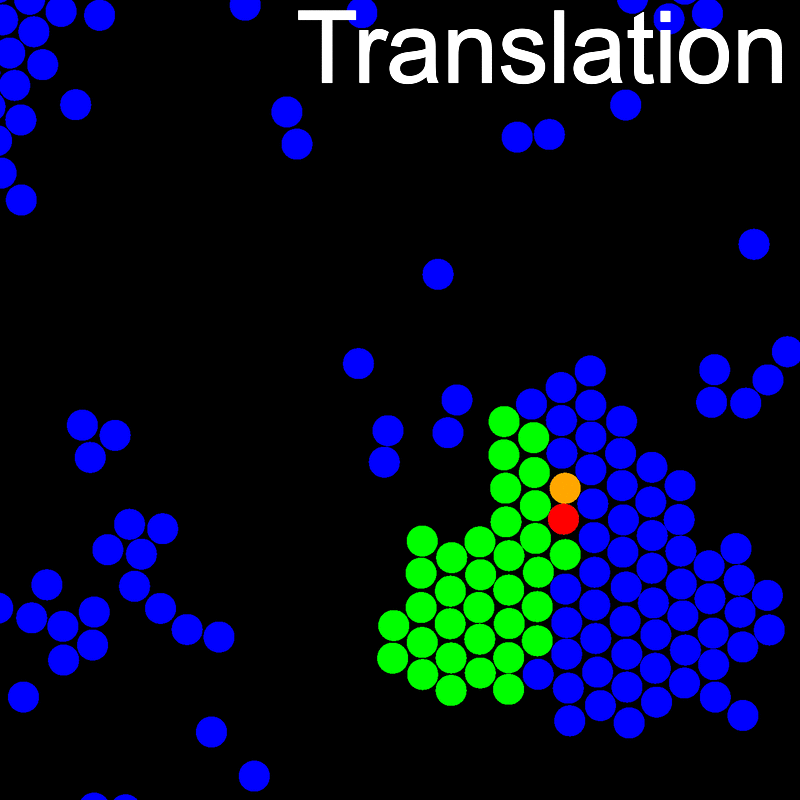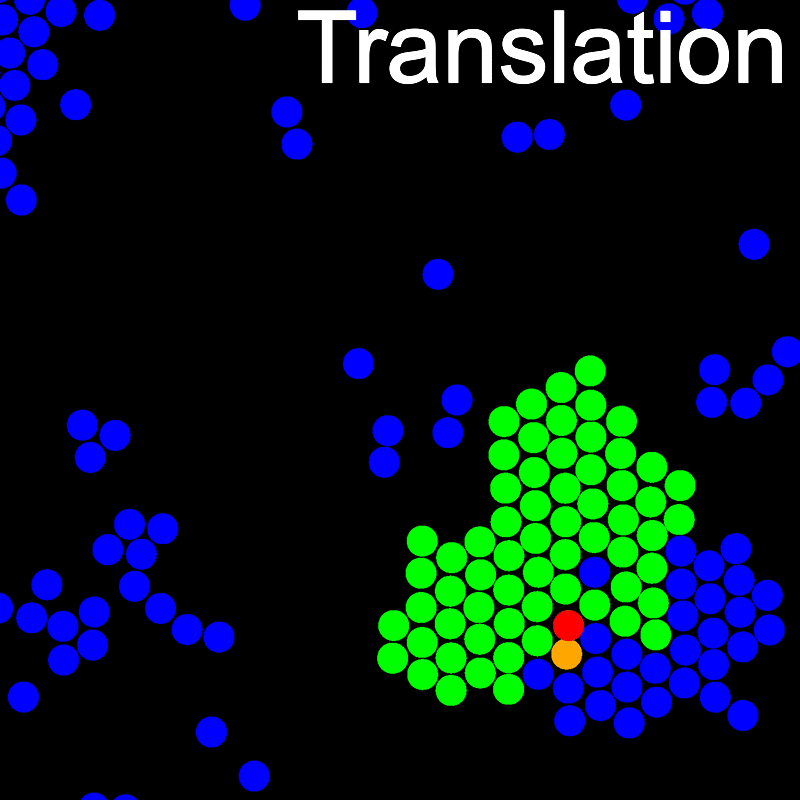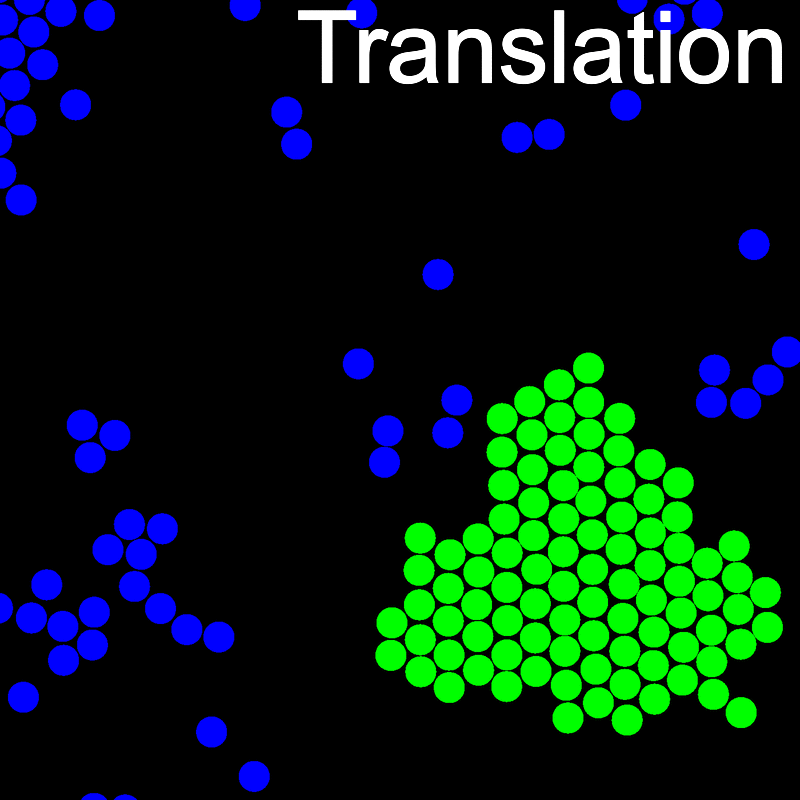
Installation
A Makefile is included for building and installing LibVMMC.
To compile LibVMMC, then install the library, documentation, and demos:
make build
make installBy default, the library installs to /usr/local. Therefore, you may need admin
priveleges for the final make install step above. An alternative is to change
the install location:
make PREFIX=MY_INSTALL_DIR installPython demos are build against Python 3.7. To use a different version of Python, run, e.g:
make PYTHON=3.9 build(Python 2 is no longer supported.)
Further details on using the Makefile can be found by running make without a target, i.e.
makeWindows users
Although intended to be used on a Unix-like operating system, LibVMMC works fine on Windows using MinGW. For modern, 64-bit Windows systems, we recommend using MYSYS2. This has been used to successfully build on Windows 7 and 10. After installing MYSYS2 (following the instructions on the website) you will need to install several additional packages:
pacman -S gcc git make python diffutilsYou can now clone the repository and build LibVMMC as follows:
updatedb
git clone https://github.com/lohedges/vmmc
cd vmmc
make build
Compiling and linking
To use LibVMMC with a C/C++ code first include the LibVMMC header file somewhere in the code.
//example.cpp
#include <vmmc/VMMC.h>Then to compile, we can use something like the following:
g++ -std=c++11 example.cpp -lvmmcThis assumes that we have used the default install location /usr/local. If
we specify an install location, we would use a command more like the following:
g++ -std=c++11 example.cpp -I/my/path/include -L/my/path/lib -lvmmcNote that the -std=c++11 compiler flag is needed for std::function and
std::random.
Dependencies
LibVMMC uses the Mersenne Twister
pseudorandom number generator. A C++11 implementation using std::random is
included as a bundled header file, MersenneTwister.h. See the source code or
generate Doxygen documentation with make doc for details on how to use it.
Callback functions
LibVMMC works via several user-defined callback functions that abstract model
specific details, such as the pair potential. We make use of C++11's
std::function to provide a general-purpose function wrapper, i.e.
the callbacks can be free functions, member functions, etc. These callbacks
allow LibVMMC to be blind to the implementation of the model, and likewise
the model to be blind to the details of the VMMC algorithm. The generic
nature of the function wrapper provides great flexibility to the user, freeing
them from a specific design choice for the model in hand. It is possible to
glue together components written in different ways, or to use the callbacks
themselves as C/C++ wrappers to external libraries.
An alternative version of LibVMMC that shows how to achieve the same callback
functionality using a pure abstract Model base class can be found in the
pure-abstract branch. While this provides a cleaner interface, the additional
flexibility provided by std::function more than offsets the minimal
performance cost.
Details of the callback prototypes are given below (where typedef has
been used to simplify their declaration). The const keyword is used to
aid readability and to prevent the user from modifying particle positions
and orientations. (For those unfamiliar with C/C++, const double* p_double
means that you can't modify the data pointed to by p_double although you
can change what p_double points to.) For simplicity we make use of the
"pointer to type" representation of array data, i.e. all pointer arguments in the
callback prototypes represent arrays.
Particle energy
Calculate the total pair interaction energy felt by a particle.
typedef std::function<double (unsigned int index, const double* position,
const double* orientation)> EnergyCallback;index = The particle index.
position = An x, y, z (or x, y in 2D) coordinate vector for the particle.
orientation = The particle's orientation unit vector.
This callback function is currently somewhat redundant since it is possible to
achieve the same outcome by combining the PairEnergyCallback and
InteractionsCallback functions described below.
Pair energy
Calculate the pair interaction between two particles.
typedef std::function<double (unsigned int index1, const double* position1,
const double* orientation1, unsigned int index2, const double* position2,
const double* orientation2)> PairEnergyCallback;index1 = The index of the first particle.
position1 = The coordinate vector of the first particle.
orientation1 = The orientation unit vector of the first particle.
index2 = The index of the second particle.
position2 = The coordinate vector of the second particle.
orientation2 = The orientation unit vector of the second particle.
Interactions
Determine the interactions for a given particle.
typedef std::function<unsigned int (unsigned int index, const double* position,
const double* orientation, unsigned int* interactions)> InteractionsCallback;index = The index of the particle.
position = The coordinate vector of the particle.
orientation = The orientation unit vector of the particle.
interactions = An array to store the indices of the interactions.
Post-move
Apply any post-move updates, e.g. update cell lists, or neighbour lists.
typedef std::function<void (unsigned int index, const double* position,
const double* orientation)> PostMoveCallback;index = The index of the particle.
position = The coordinate vector of the particle following the move.
orientation = The orientation unit vector of the particle following the move.
Non-pairwise energy (optional)
Test for non-pairwise energy contributions, such as interactions with a surface or external field.
typedef std::function<double (unsigned int, const double* position,
const double* orientation)> NonPairwiseCallback;index = The index of the particle.
position = The coordinate vector of the particle.
orientation = The orientation unit vector of the particle.
Boundary condition (optional)
Test for a custom boundary condition. This should return true if the particle moves outside of the boundary following the virtual move. An example showing how to implement custom boundary conditions is provided with the demonstration code.
typedef std::function<bool (unsigned int index, const double* position,
const double* orientation)> BoundaryCallback;index = The index of the particle.
position = The coordinate vector of the particle following the move.
orientation = The orientation unit vector of the particle following the move.
Assigning a callback
Using the callbacks above it is easy to create a function wrapper to whatever, e.g.
vmmc::EnergyCallback energyCallback = computeEnergy;if computeEnergy were a free function, or
Foo foo;
using namespace std::placeholders;
vmmc::EnergyCallback energyCallback = std::bind(&Foo::computeEnergy, foo, _1, _2, _3);if computeEnergy were instead a member of some object called Foo.
For simplicity we provide a container for callback functions. This simplifies assignment and makes it possible to pass a single callback argument to the constructor of the VMMC object.
struct CallbackFunctions
{
EnergyCallback energyCallback;
PairEnergyCallback pairEnergyCallback;
InteractionsCallback InteractionsCallback;
PostMoveCallback postMoveCallback;
NonPairwiseCallback nonPairwiseCallback;
BoundaryCallback boundaryCallback;
};In the second example above, initialisation of the energyCallback function would become
Foo foo;
using namespace std::placeholders;
vmmc::CallbackFunctions callbacks;
callbacks.energyCallback = std::bind(&Foo::computeEnergy, foo, _1, _2, _3);The VMMC object
To use LibVMMC you will want to create an instance of the VMMC object. This has the following constructor:
VMMC(unsigned int nParticles, unsigned int dimension, double* coordinates,
double* orientations, double maxTrialTranslation, double maxTrialRotation,
double probTranslate, double referenceRadius, unsigned int maxInteractions,
double* boxSize, bool* isIsotropic, bool isRepulsive,
const CallbackFunctions& callbacks);nParticles = The number of particles in the simulation box, \(N\).
dimension = The dimension of the simulation box (either 2 or 3).
coordinates = An array containing coordinates for all of the particles in the
system, i.e. \(x_1, y_1, z_1, x_2, y_2, z_2, \ldots , x_N, y_N, z_N.\)
Coordinates should run from 0 to the box size in each dimension.
orientations = An array containing orientations (unit vectors) for all of the
particles in the system, i.e. \(\hat{x}_1, \hat{y}_1, \hat{z}_1, \hat{x}_2, \hat{y}_2, \hat{z}_2, \ldots , \hat{x}_N, \hat{y}_N, \hat{z}_N.\)
In the case of particles interacting via an isotropic potential, the particle
orientations are entirely redundant, i.e. the orientation has no effect on the
potential. This allows the use of a single set of callback functions for models
with both isotropic and anisotropic potentials.
maxTrialTranslation = The maximum trial translation, in units of the particle
diameter (or typical particle size).
maxTrialRotation = The maximum trial rotation in radians.
probTranslate = The probability of attempting a translation move (relative to rotations).
Along with maxTrialTranslation and maxTrialRotation, probTranslate can be tuned to
enforce an approximate Stokes drag. An excellent and detailed explanation of how this may
be applied in practice can be found
here.
referenceRadius = A reference radius for computing the approximate hydrodynamic
damping factor, e.g. the radius of a typical particle in the system. When
modeling a molecular system the reference radius should indicate the
approximate radius of a single molecular unit.
maxInteractions = The maximum number of pair interactions that an individual
particle can make. This will be used to resize LibVMMC's internal data
structures and the user should assert that this limit isn't exceed in the
InteractionsCallback function. The number can be chosen from the symmetry
of the system, e.g. if particles can only make a certain number of patchy
interactions, or by estimating the average number of neighbours within the
interaction volume around a particle.
boxSize = The base length of the simulation box in each dimension.
isIsotropic = Whether the potential of each particle is isotropic. The
handling of rotational moves is slightly different for moves seeded from
isotropic particles, e.g. spheres, since the rotation of the seed causes
no change in energy. This boolean array allows LibVMMC to handle
mixed-potential systems.
isRepulsive = Whether the potential has finite energy repulsions. This should
also be set to true when particle interactions contain a mixture of hard core
overlaps and finite repulsions.
callbacks = The callback function container.
C-style arrays
The VMMC object constructor and callback functions use C-style arrays as
arguments for simplicity and generality. This (hopefully) makes it as easy
as possible for a user unfamiliar with C++ to make use of LibVMMC (although
everyone should take time to learn std::vector). We can also exploit the
fact that the C++ standard imposes that std::vector elements are contiguous,
which allows std::vector containers to be passed as naked arrays.
For example, if we have some function called foo that accepts a C-style
double array as an argument,
void foo(double* arr); // or alternatively, void foo(double[]);then both of the following are valid function calls
// C style
double c_arr[10];
foo(c_arr);
// C++ style
std::vector<double> cpp_arr(10);
foo(&cpp_arr[0]);Internally, LibVMMC uses std::vector containers for its data structures, with
data passed to the callback functions in the manner described above.
Units
Energies returned by the callback functions should be in units of Boltzmann's constant multiplied by temperature, i.e. \(k_{\rm{B}}T\). Distances are measured in units of the particle (or molecular) diameter, \(\sigma\). In the demonstration code we take the statistical mechanician's prerogative of setting both \(k_{\rm{B}}T\) and \(\sigma\) equal to one.
Executing a virtual move
Once an instance of the VMMC object is created, e.g.
VMMC(...) vmmc;then a single trial move can be executed as follows:
vmmc.step();To perform 1000 trial moves:
vmmc.step(1000);The same can be achieved by using the overloaded ++ and += operators,
i.e. vmmc++ for a single step, and vmmc += 1000 for 1000 steps.
Demos
The following example codes showing how to interface with LibVMMC are included
in the demos directory.
-
square_wellium.cpp: A simulation of a square-well fluid in two- or three-dimensions. -
square_wellium_wall.cpp: A simulation of a square-well fluid interacting with a wall in two- or three-dimensions. -
square_wellium_spherocylinder.cpp: A simulation of a three dimensional square-well fluid confined within an inert spherocylinder. -
patchy_disc.cpp: A simulation of a two dimensional patchy disc model.
lennard_jonesium.cpp: A simulation of a Lennard-Jones fluid in two- or three-dimensions.
When run, each of the demos output a trajectory file, trajectory.xyz, and a
TcL script, vmd.tcl, that can be used to set camera and particle attributes
and to draw the periodic simulation box when visualising the trajectory with
VMD. To generate and view a trajectory,
run, e.g.
./demos/square_wellium
vmd trajectory.xyz -e vmd.tclNote that the trajectories are intended to be used for visualisation purposes only. The atomic coordinates are not saved to file with enough accuracy for them to reliably be used as restart files, i.e. overlaps may occur.
The following animation shows example trajectories generated by a selection of the demos.
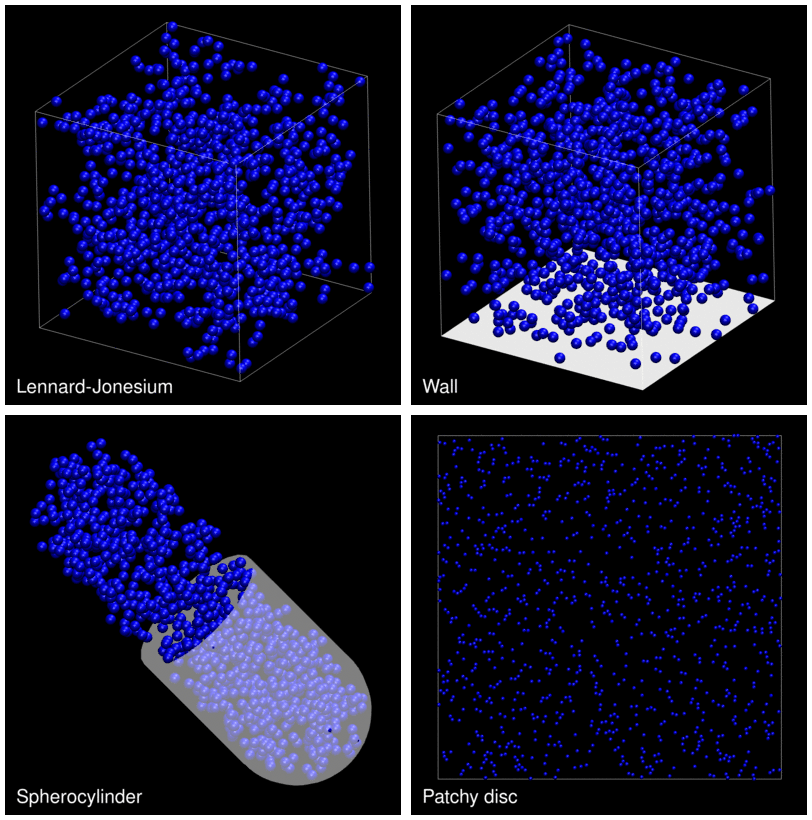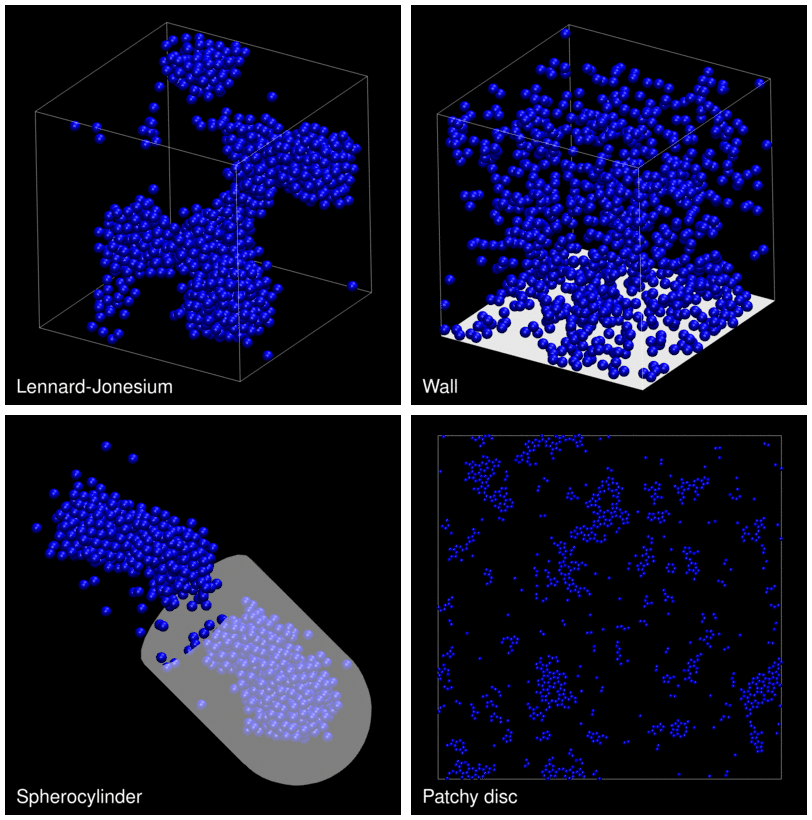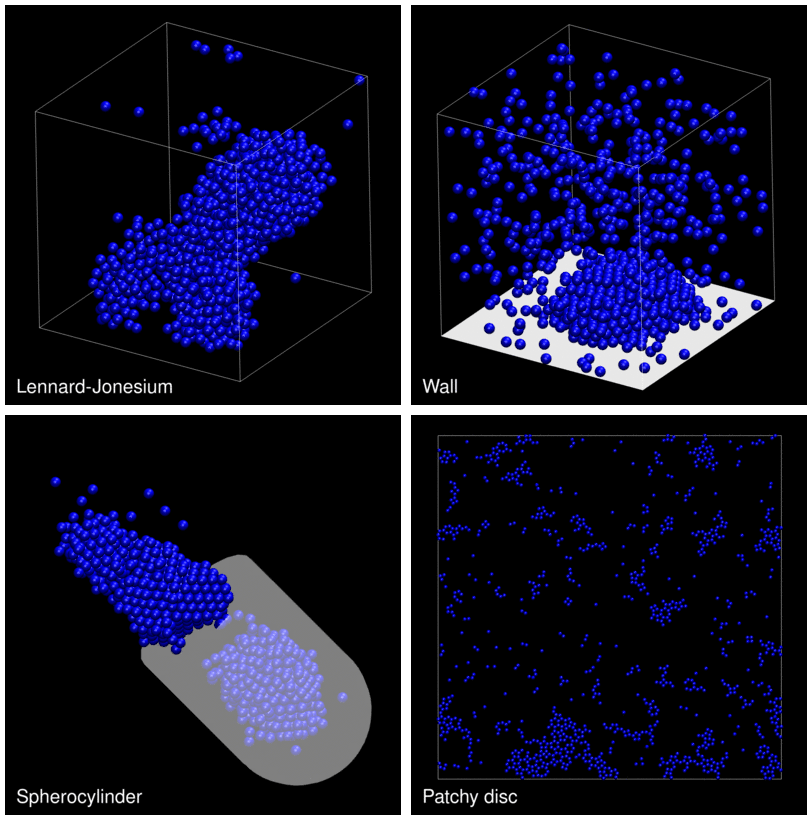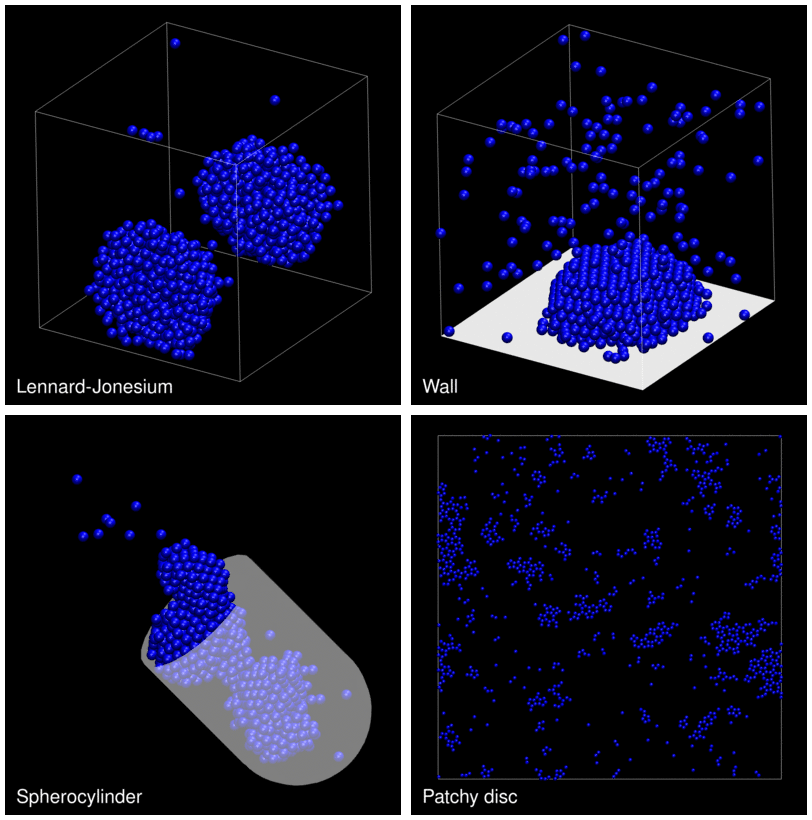
The demo code also illustrates how to implement efficient, dynamically
updated cell lists. See demos/src/CellList.h and demos/src/CellList.cpp
for implementation details. If you are simulating a system of highly size asymmetric particles,
then it might be preferable to search for interactions using a more efficient data structure,
such as a bounding volume hierarchy.
Also included in the demos/python directory are examples showing how to
interface with Python code via the Python C API.
Note that this code is intended to be used for illustrative purposes and
avoids the use of additional dependencies (e.g. NumPy).
As such, it is likely that performance could be significantly improved.
Tests
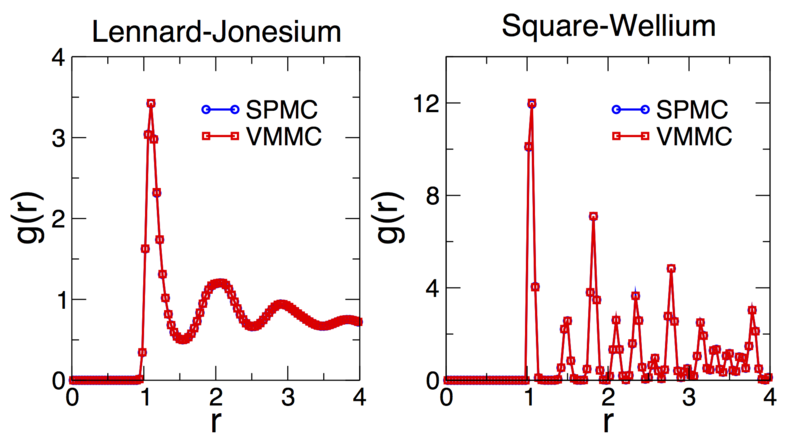
A full test suite is forthcoming. This will allow a detailed comparison between VMMC and standard single-move Monte Carlo (SPMC) for various model systems at a range of state points.
Shown below are time-averaged pair distribution functions for Lennard-Jonesium
and the square-well fluid taken from configurations equilibrated using the demo
codes outlined above (although run for 10 times as long). In both cases the
equilibrated structures are indistinguishable from those generated by SPMC.
Note that the pair distribution functions don't converge to one at large
particle separations since we are not considering a bulk system, rather a
finite cluster in a background vapour. See the demo codes
demos/lennard_jonesium.cpp and demos/square_wellium.cpp for details
of the interaction parameters (Lennard-Jonesium is sampled in the liquid
phase, the square-well fluid is sampled in the crystal (FCC/HCP) phase).
Defining a model
The demo code illustrates a simple way of defining and handling different model
potentials. A base class, Model, is used to declare default functionality and
callbacks. Derived classes, such as LennardJonesium, are used to implement the
model specific pair potential, which is declared as a virtual method in the base
class.
Declaring a new user-defined model should be as easy as creating a UserModel
class with public inheritance from the Model base class, then overriding
the virtual computePairEnergy method. The LennardJonesium, SquareWellium,
and PatchyDisc classes will serve as useful templates.
Pure isotropic systems
The default build of LibVMMC provides support for systems of isotropic and anisotropic particles, or mixtures of both. However, in the case of pure isotropic systems, e.g. spherical particles interacting via a spherically symmetric potential, such as the square-well fluid, particle orientations are entirely redundant since they have no bearing on the potential. This means that there is no need to pass orientations as arguments to callback functions, or to update particle orientations during VMMC trial moves.
We provide preprocessor directives that allow LibVMMC to be compiled as an optimised library for pure isotropic systems. This can be achieved as follows:
make OPTFLAGS=-DISOTROPIC buildThe isotropic version of LibVMMC provides a simplified set of callback
functions that require no particle orientations. For example, the
PairEnergyCallback becomes
typedef std::function<double (unsigned int index1, const double* position1,
unsigned int index2, const double* position2)> PairEnergyCallback;In addition, the VMMC object no longer needs the orientations or
isIsotropic arrays to be passed to its constructor, which is simplified to
VMMC(unsigned int nParticles, unsigned int dimension, double* coordinates,
double maxTrialTranslation, double maxTrialRotation, double probTranslate,
double referenceRadius, unsigned int maxInteractions, double* boxSize,
bool isRepulsive, const CallbackFunctions& callbacks);The demo code shows how preprocessor directives can be used to provide support
for either version of the library, e.g. for the default computeEnergy callback
defined in the Model class, we have
#ifndef ISOTROPIC
virtual double computeEnergy(unsigned int, const double*, const double*);
#else
virtual double computeEnergy(unsigned int, const double*);
#endifThe pure isotropic version of LibVMMC can provide a significant performance gain when executing rotations of large clusters in isotropic systems.
Note that the demo patchy_disc.cpp will not compile against the isotropic
version of the library since the model is anisotropic and requires
particle orientations to be passed to its callback functions.
Limitations
- The calculation of the hydrodynamic damping factor assumes a spherical cluster, which is only approximate in two dimensions. In general, it is likely that particles on a flat surface may diffuse in a system-specific way, so there may be no good general approximation of Stokes scaling in two dimensions. In future versions we intend to provide an additional callback function so that the user can enforce a model-specific damping factor.
- The recursive manner in which the trial cluster is built can lead to a stack overflow if the cluster contains many particles. Typically, thousands, or tens of thousands of particles should be perfectly manageable. The typical memory footprint for a simulation of 1000 particles is around 2.5MB for hard particles. This is roughly doubled if the potential has finite energy repulsions.
Efficiency
In aid of generality there are several sources of redundancy that impact the efficiency of the VMMC implementation. As written, LibVMMC performs around 3-4 times worse than a fully optimised VMMC code for square-well fluids. A few efficiency considerations are listed below in case the user wishes to modify the VMMC source code in order to improve performance.
- When calculating a list of neighbours with which a given particle interacts it's likely that you'll need to calculate the pair interaction energy. For certain models it may be more efficient to return a list of pair energies along with the interactions, rather than having to recalculate them.
- For models with an isotropic interaction of fixed energy scale the pair energy is simply a constant. As such, the pair energy calculation is entirely redundant, i.e. knowing that two particles interact is enough to know the pair energy.
- If using cell lists, the typical size of a trial displacement will be small
enough such that a particle stays within the same neighbourhood of cells
following the trial move. (This isn't necessarily true for rotation moves,
where the displacement of particles far from the rotation axis can be large.)
As such, there is often no need to update cell lists until confirming that
the post-move configuration is valid, e.g. no overlaps. At present the same
PostMoveCallbackfunction is called twice: once in order to apply the move; again if the move is subsequently rejected. This means that the cell lists will be updated twice if a move is rejected. - When testing for particle overlaps following a virtual move it is normally not necessary to test pairs within the moving cluster. As written, all links are tested, not just those external to the cluster. Note that all internal pairs should be tested following a rotational move since it's possible to rotate a cluster on top of itself. This can occur in a dense system when one axis of a cluster is longer than the box size, e.g. the cluster lies diagonally in a square box. In this case, a rotation across the periodic boundary can cause the cluster to overlap.
- Due to the overhead of binding member functions it is marginally faster to use free functions as callbacks.
Tips
- It is not a requirement that all particles in the simulation box be of the same type. Make use of the particle indices that are passed to callback functions in order to distinguish different species.
Help
To help new users, some common pitfalls are listed below.
- LibVMMC uses a cuboidal simulation box with a centre at \((L_x/2, L_y/2, L_z/2)\), where \(Lx\), \(Ly\), and \(Lz\) are the box lengths in each dimension. As such, particle positions must run from 0 to the box size in each dimension. If you require a different box format, e.g. the centre at \((0, 0, 0\)), which is typical in NPT simulations for simplifying changes to the box volume, then simply shift the coordinates inside of the callback functions.
- Particle orientations must be specified as unit vectors. While this might not be the most efficient representation for your model, it is easy to generalise and provides a consistent representation in two and three dimensions. If you require an alternative representation then you'll need to provide support for converting between orientation formats.
Citing LibVMMC
If you make use of LibVMMC in any published research please cite the canonical VMMC reference:
- Avoiding unphysical kinetic traps in Monte Carlo simulations of strongly attractive particles,S. Whitelam and P.L. Geissler, Journal of Chemical Physics, 127, 154101 (2007)
and the symmetrised version of the algorithm described in the appendix of
- The role of collective motion in examples of coarsening and self-assembly, S. Whitelam, E.H. Feng, M.F. Hagan, and P.L. Geissler, Soft Matter, 5, 1251 (2009)
Please also include a citation to the official LibVMMC page:
A properly formatted BibTex file is provided here.
Disclaimer
Please be aware that this a working repository so the code should be used at your own risk. At present the code is being tested so expect that it will be updated fairly frequently with additional features and performance enhancements.